【課題】グローバーアルゴリズムを使った量子振幅推定#
グローバーアルゴリズムは求める答えの位相を反転させるという操作を行うことによって、構造を持たないデータベースから答えを見つけることができるというものでした。
グローバーアルゴリズムでは、 最初にアダマール演算子をかけて均等重ね合わせの状態\(\ket{s} = H^{\otimes n}\ket{0}^{\otimes n} = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\ket{x}\)を作りました。 ここでは、\(\ket{s}\)の代わりに、\(\ket{0}^{\otimes n}\)に既知のユニタリー\(U\)を適用して作った状態\(\ket{\psi}=U\ket{0}^{\otimes n}\)を持ってくるとしましょう。
この状態\(\ket{\psi}\)は求める答え\(\ket{w}\)の成分を含んでいますが、その振幅が分からないとします。 つまり、 ここで使った2次元平面での記述方法に従うと、\(\ket{\psi}\)も\(\ket{s}\)と同じく
と書くことができますが、\(\ket{w}\)の振幅である\(\sin\frac\theta2\)の\(\theta\)の値が分からないという状況です。
この書き方に従えば、求める状態は\(\ket{w}=\begin{bmatrix}0\\1\end{bmatrix}\)、それに直交する状態は\(\ket{w^{\perp}}=\begin{bmatrix}1\\0\end{bmatrix}\)だったので、 オラクル\(U_w\)は前と同じく\(U_w=I-2\ket{w}\bra{w}=\begin{bmatrix}1&0\\0&-1\end{bmatrix}\)です。\(U_0=2\ket{0}\bra{0}^{\otimes n}-I\)なので、均等重ね合わせ\(\ket{s}\)の場合はDiffuser \(U_s\)は
でしたが、今は\(\ket{\psi}\)としているため
になります。\(\theta\)を使った行列表記は\(\ket{s}\)の場合と同じです。
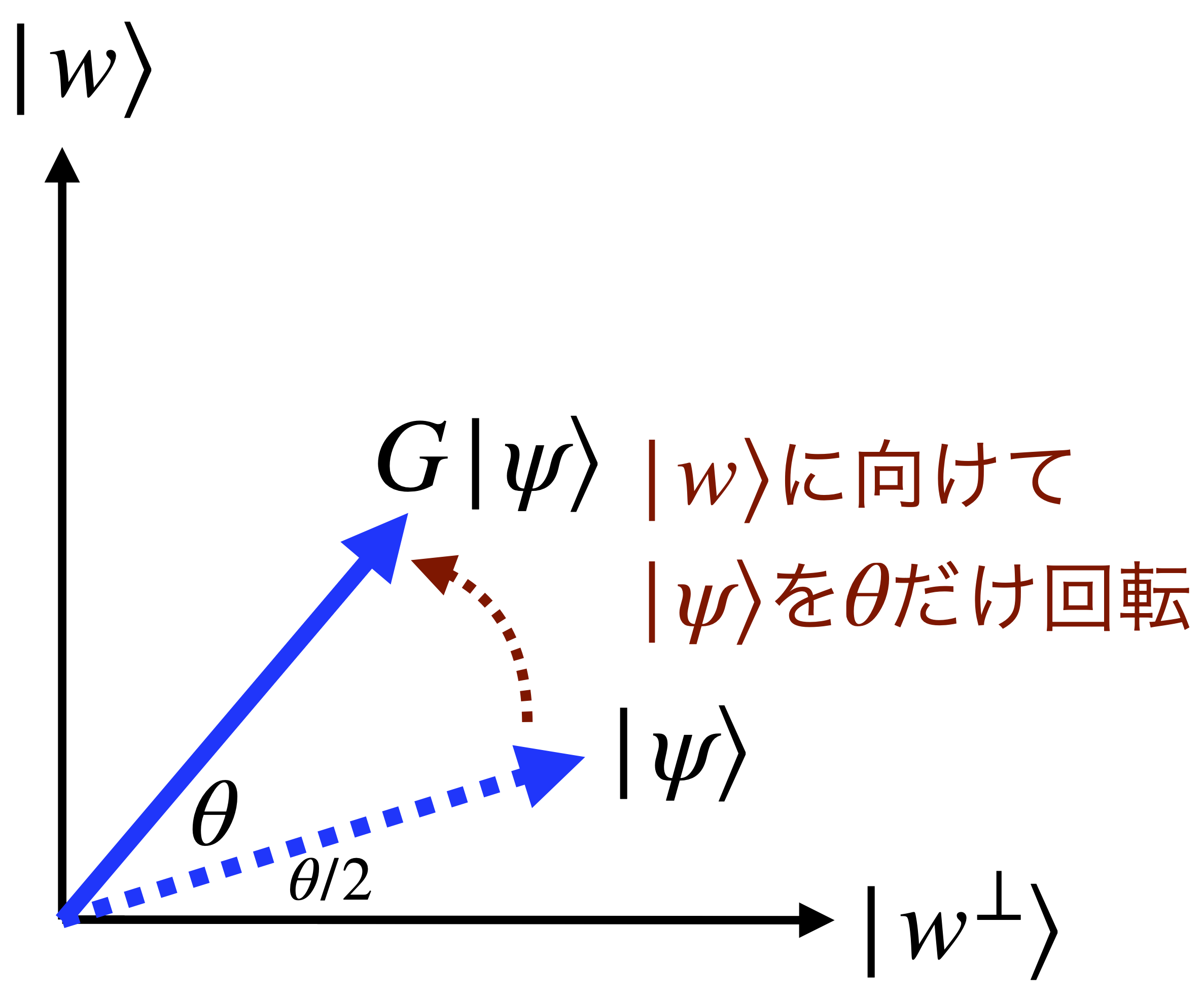
つまり下図にある通り、\(\ket{\psi}=\cos\frac\theta2\ket{w^{\perp}}+\sin\frac\theta2\ket{w}\)と書けている場合、\(G\)は\(\ket{\psi}\)を\(\ket{w}\)に向かって角度\(\theta\)だけ回転するという訳で、グローバーアルゴリズムと同じ操作になっています。
量子振幅推定#
グローバーのアルゴリズムと量子位相推定の方法を組み合わせることで、量子状態\(\ket{\psi}\)の振幅を推定することができます。この方法は量子振幅推定と呼ばれ、その基本的な方法は最初にこの論文[BHMT00]で提案されました。
まず、グローバーの反復\(G\)が\(\ket{\psi}\)を\(\ket{w}\)に向かって角度\(\theta\)回転するということをよりクリアに見るため、 \(\ket{w}\)と\(\ket{w^{\perp}}\)を使って
と書ける状態\(\ket{\psi_{\pm}}\)を考えてみます。この状態に\(G\)を適用するわけですが、 \(G=U_sU_w\)が
と書けることを思い出すと、
となります。なので、\(\ket{\psi_{\pm}}\)に\(G\)を適用すると
となります。つまり\(\ket{\psi_{\pm}}\)は\(G\)の固有ベクトルで、\(e^{\pm i\theta}\)はその固有値です。 これは\(\ket{\psi}\)が\(G\)の固有ベクトルそのものになっているケースですが、 量子位相推定の実習で見たように、準備する状態\(\ket{\psi}\)が固有ベクトルの成分を含む形になっていれば、効率は下がりますが、量子位相推定が使えると予想できそうです。
このことから、(\(\ket{w}\)を含む)状態\(\ket{\psi}\)を準備して、その状態にグローバーの反復\(G\)を作用させて量子位相推定を行えば、固有値の位相として角度\(\theta/(2\pi)\)を求めることができそうです。この角度が分かれば、求める答え\(\ket{w}\)の振幅\(\sin\frac\theta2\)を推定することができます。これが量子振幅推定と呼ばれる方法です。
問題設定#
この課題では、振幅が分かっている状態を前もって準備しておくことにします。その状態に量子振幅推定のための量子回路を適用して、振幅が正しく評価できることを示してもらいます。
Qiskitでの実装#
まず必要な環境をセットアップします。
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import Math
# Qiskit関連のパッケージをインポート
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit_aer import AerSimulator
# ワークブック独自のモジュール
from qc_workbook.show_state import statevector_expr
状態準備として、 3量子ビットの回路でGHZ状態を作ることにします。求める答えの状態\(\ket{w}\)を\(\ket{111}\)として、この状態の振幅が\(\sin\frac\theta2\)となる状態
を生成する量子回路を作ります。\(\theta\)の値は\(\theta=\frac{\pi}{3}\)とします。
n_state = 3
##################
### EDIT BELOW ###
##################
# |psi(theta=pi/3)>を作る回路(state_prep)を書いてください
#state_prep = ...
##################
### ABOVE BELOW ###
##################
state_prep.draw('mpl')
次に、state_prepで状態を作って確認します。
simulator = AerSimulator(method='statevector')
def get_statevector_array(circuit):
# 渡された回路のコピーを使う
circuit = circuit.copy()
# 量子回路の終状態の状態ベクトルを保存するインストラクション
circuit.save_statevector()
# 再び「おまじない」のtranspileをしてから、run()に渡す
circuit = transpile(circuit, backend=simulator)
job = simulator.run(circuit)
result = job.result()
qiskit_statevector = result.data()['statevector']
# result.data()['statevector']は通常の配列オブジェクト(ndarray)ではなくqiskit独自のクラスのインスタンス
# ただし np.asarray() で numpy の ndarray に変換可能
return np.asarray(qiskit_statevector)
statevector = get_statevector_array(state_prep)
expr = statevector_expr(statevector)
Math(expr)
次にオラクル \(U_w\)とDiffuser \(U_s\)を作る回路を書いて、それらからグローバーの反復\(G=U_sU_w\)の量子回路を作ってください。
oracle = QuantumCircuit(n_state)
diffuser = QuantumCircuit(n_state)
##################
### EDIT BELOW ###
##################
# Groverの反復を行う回路を書いてください
#grover_iter = ...?
##################
### ABOVE BELOW ###
##################
grover_iter.decompose().draw('mpl')
量子位相推定の回路は以下のようにします。読み出しレジスタqreg_readoutを制御ビットとして、制御Gゲートを状態レジスタqreg_statusに適用する回路を書いてください。
# 読み出しレジスタの量子ビット数
n_readout = 4
# 読み出しレジスタ
qreg_readout = QuantumRegister(n_readout, name='readout')
# 状態レジスタ
qreg_state = QuantumRegister(n_state, name='state')
# 読み出し結果が書き出される古典レジスタ
creg_readout = ClassicalRegister(n_readout, name='out')
# 2つの量子レジスタと1つの古典レジスタから量子回路を作る
qc = QuantumCircuit(qreg_readout, qreg_state, creg_readout)
# それぞれのレジスタを初期化
qc.h(qreg_readout)
qc.barrier()
# 状態準備の回路state_prepを固有ベクトルを保持するレジスタに入れる
qc.append(state_prep, qargs = qreg_state)
qc.barrier()
##################
### EDIT BELOW ###
##################
# 読み出しレジスタを制御ビットとして、制御Gゲートを状態レジスタに適用する回路を書いてください。
##################
### ABOVE BELOW ###
##################
逆量子フーリエ変換の回路は以下のものを使います。
def qft_dagger(qreg):
"""逆量子フーリエ変換用の回路"""
qc = QuantumCircuit(qreg)
for j in range(qreg.size // 2):
qc.swap(qreg[j], qreg[-1 - j])
for itarg in range(qreg.size):
for ictrl in range(itarg):
power = ictrl - itarg - 1
qc.cp(-2. * np.pi * (2 ** power), ictrl, itarg)
qc.h(itarg)
qc.name = "QFT^dagger"
return qc
qc.barrier()
# 読み出しレジスタに逆フーリエ変換の回路を追加
qc.append(qft_dagger(qreg_readout), qargs = qreg_readout)
qc.barrier()
qc.measure(qreg_readout, creg_readout)
qc.draw('mpl')
シミュレータで実行して、結果を確かめましょう。
from qiskit.primitives import Sampler
sampler = Sampler()
# Now run the job and examine the results
sampler_job = sampler.run(qc)
result = sampler_job.result()
from qiskit.visualization import plot_distribution
plt.style.use('dark_background')
plot_distribution(result.quasi_dists[0])
提出するもの
以下を行う回路
状態を準備する
グローバーの反復Gを行う
読み出しレジスタを制御ビットとして、制御Gゲートを状態レジスタに適用する
量子振幅推定を行った結果のヒストグラムと、その解釈
